Quantum reservoir neural network implementation on a Josephson Parametric Converter.
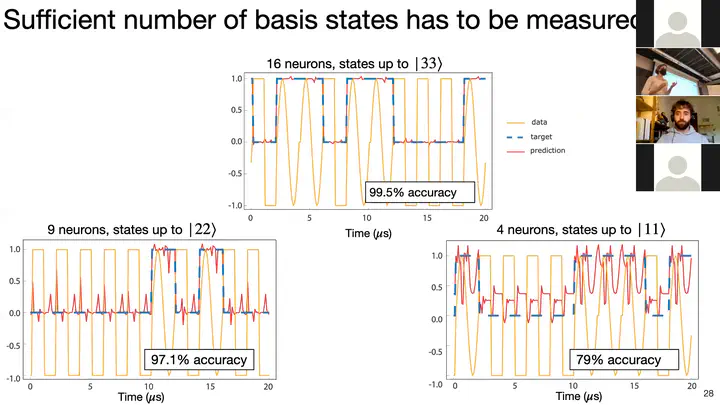 Image credit: Unsplash
Image credit: Unsplash
Neuromorphic computing implements neural networks in hardware to make their training more time and energy efficient. However, addressing state-of-the-art machine learning tasks requires coupling large numbers of neurons, which is challenging with physical nano-devices. It has been proposed to solve this problem using quantum hardware and encoding neurons in the basis states, whose number is exponential in the number of coupled qubits. Simulation of a neural network called a quantum reservoir, implemented on a small number of qubits, showed that this quantum neural network can solve certain learning tasks with fewer neurons than an equivalent classical reservoir 1.
In this work, in order to obtain an even larger number of basis states, we use quantum oscillators instead of qubits. To go towards an experimental realization, we simulate a reservoir neural network implemented on a Josephson parametric converter, a well known quantum superconducting circuit. This circuit couples two superconducting oscillators through a three-wave-mixing interaction, implemented using a ring of four Josephson junctions. We encode the input data in the resonant oscillators’ drives and numerically integrate quantum master equation to find the occupation probabilities of a subset of basis states that represent neural network outputs. We show that this system of two coupled quantum oscillators can solve a sine and square waveform classification task that otherwise requires 25 classical oscillators 2. Furthermore, in order to test its memory, we train this network to perform chaotic time series prediction and show that with typical experimental parameters for a Josephson parametric converter we can obtain performance comparable to other physical neural networks.
These results show that a simple and well known quantum circuit can realize non-trivial machine learning tasks when its dynamics is exploited. Neuromorphic computing thus promises to leverage the full computing capabilities of even small quantum systems. These simulations will guide experimental realization of a reservoir neural network on the Josephson parametric converter.