Contextuality in entanglement-assisted one-shot classical communication

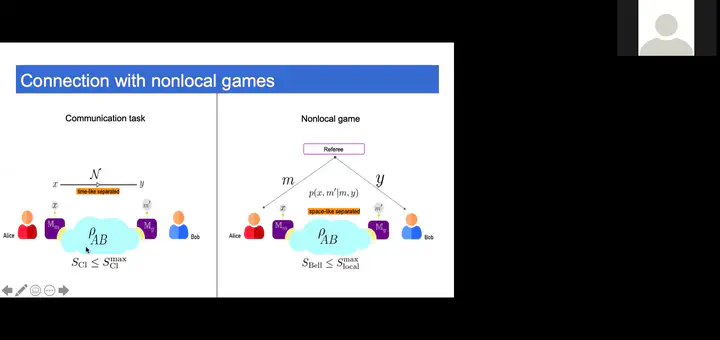
We consider the problem of entanglement-assisted one-shot classical communication. In the zero-error regime, entanglement can increase the one-shot zero-error capacity of a family of classical channels following the strategy of Cubitt et al., Phys. Rev. Lett. 104, 230503 (2010). This strategy uses the Kochen-Specker theorem which is applicable only to projective measurements. As such, in the regime of noisy states and/or measurements, it cannot increase the capacity. To accommodate generically noisy situations, we examine the one-shot success probability of sending a fixed number of classical messages. We show that preparation contextuality powers the quantum advantage in this task, increasing the one-shot success probability beyond its classical maximum. We then show a mapping between this communication task and a corresponding nonlocal game. This mapping generalizes the connection with pseudo-telepathy games previously noted in the zero-error case. Finally, after motivating a constraint we term context-independent guessing, we show that the contextuality witnessed by noise-robust noncontextuality inequalities obtained in R. Kunjwal, Quantum 4, 219 (2020), is sufficient for enhancing the one-shot success probability. This provides an operational meaning to these inequalities and the associated hypergraph invariant, the weighted max-predictability. The task of entanglement-assisted one-shot classical communication thus provides a fertile ground to study the interplay of the Kochen-Specker theorem, Spekkens contextuality, and Bell nonlocality.

Based on arXiv:2006.00469.